Bir sayının 11’e bölümü her zaman kolay olmayabilir
Bir sayının 11’e bölümü her zaman kolay olmayabilir. Basit bir formül sayesinde, 6-7-8-9 basamaklı sayıları bile bir çırpıda bölebilirsiniz. Tabii, burada amacımız 11 ile bölümünden kalanı bulmak olacak. Bunun için + – + – + – formülü kullanılır, örnekle nasıl yapıldığına birlikte göz atalım.
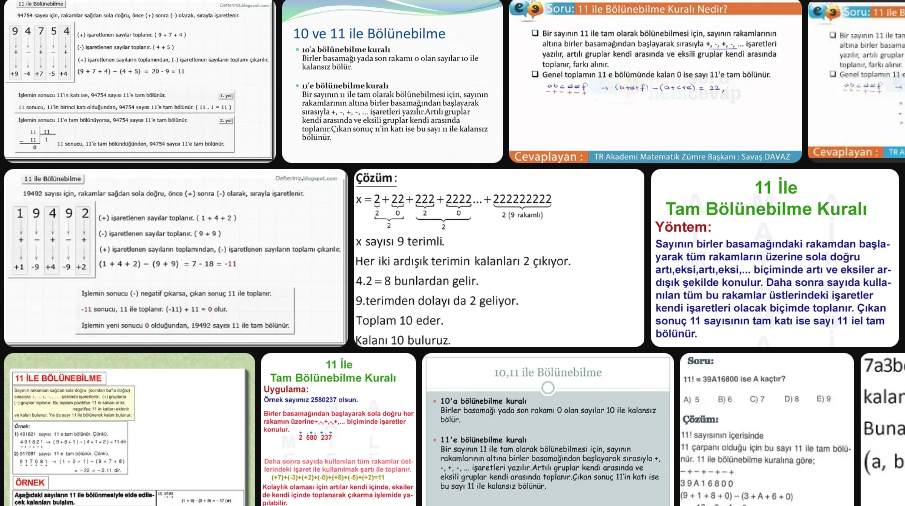
11 Bölünme Kuralı Formülü ve Örnekler
11 ile Bölünebilme
Size sınavlarda, çok basamaklı sayıların 11 ile bölümünden kalan sorulduğunda bölerek bu işlemi yaparsanız sınavda zamanınız yetmeyebilir. O yüzden kuralı bilmeniz gerekir. Soldan başlayarak + – + – şeklinde rakamlar yazılır, çıkan sonuç 0 olursa 11 e tam bölünebilir demektir. 10 çıkarsa 11 ile bölümden kalan 10 demektir. 1111 rakamından aklınızda formülü daha rahat tutarsınız. +1 -1 +1 -1 = 0 Sonuç sıfır olduğundan 11 ile tam bölünebilir.
11 ile Bölünebilme Kuralı Örnekle Anlatım
569635 = +5 -6 +9 -6 +3 -5 = 11 bu sayının 11 ile tam bölünen bir sayı olduğunu söyleyebiliriz.
671 = +6 -7 +1 = 0 sonuç sıfır çıkarsa da on bire tam bölünebilir demektir.
892548 6 basamaklı sayısı 11’e bölündüğünde kalan kaçtır?
6 basamaklı sayılar için 1-3-5. Sıradakileri ayrı 2-4-6.sıradakileri ayrı toplarsak işlemi daha kolay yapabiliriz.
Birinci üçüncü ve beşinci sıradaki rakamlar + işaretlidir ve toplanır 8 + 2 + 4 = 14
İkinci, dördüncü ve altıncı sıradakileri – işaretlidir ve çıkarılır. -9 -5 -8 =-22
14 – 22 sayısı bize -8’i verir ve 892548 6 basamaklı sayısından kalan 8 olarak bulunur. 11 ve 0 olursa tam diğer rakamlar kalanı verir.
